What is a Lie algebra, really

A geometric view
The standard view: a linear space L with a product, i.e., a bilinear map L x L ---> L denoted 

a,b ---->  [a,b]

Let us however view it as a linear space L with a (1,2)-variant tensor c. We may view c as a map 


L* x L x L ----> R
Different restrictions of this map to a fewer number of arguments result in major concepts of Lie agebra: 

Algebra product       m:    L/\L ---> L                  [v,w] = c( . ,v , w)

Co-algebra product   m*:      L* ---> L* /\ L*       m*(alpha) = c(alpha, . , . )

Adjoint map          ad:      L  ---> L x L*             ad(v) = c( . , v, . )

Tong map            tau:  L* x L ---> L*          tau(alpha,v) = c (alpha, v, . )

These maps can be put into one diagram:

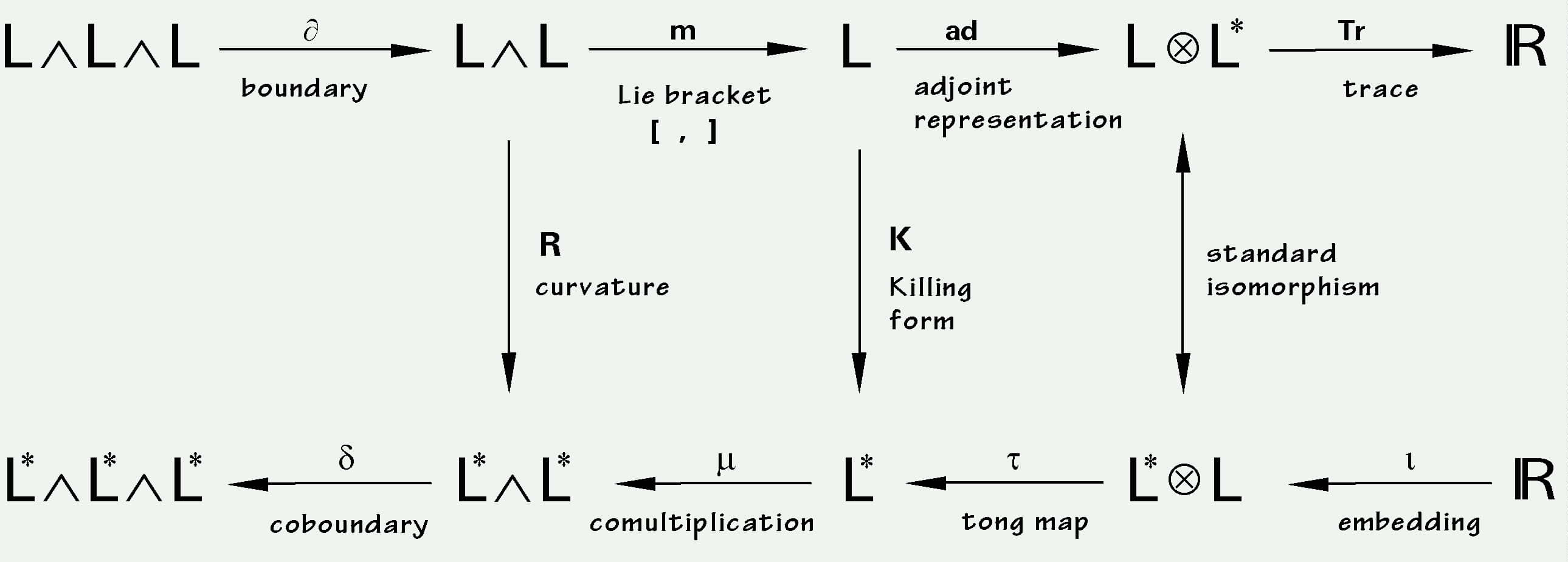
graph of a Lie map
This is the mandala of a Lie algebra.

Click here
to get to an interactive page, where you can click on a particular item
of the mandala to get further definitions.


Copyright © 1995 jerzy kocik

You may see the full-size version a of this picture (you will need to scroll the screen).

For the printing purposes download the Lie map in jpeg format 66 Kb

Lie alg
home 		Lie maps Lie mandala diff geo learn graphs HomePage of JK