This is a 3D version of the Apollonian depth fractal, introduced here. The movie shows (x,y) plane and time goes through the section along the z axis.

Geometry of relativistic   addition of velocities [1 Sep 2012]

How do you add velocities?

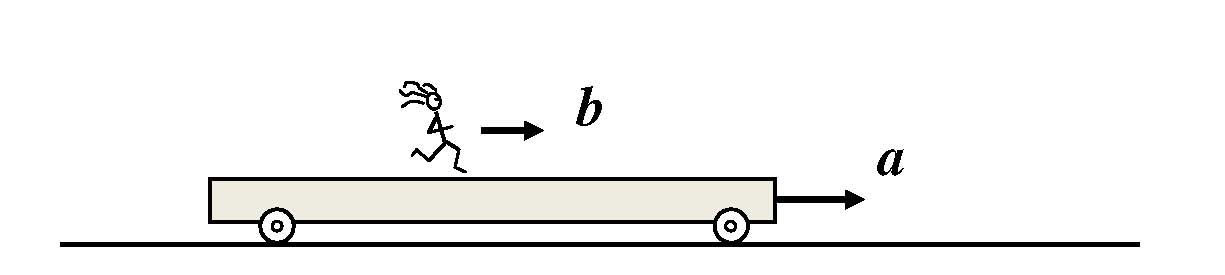
In the theory of relativity, velocities need to be added not according to the simple Galilean law:

but rather according to Poincare's formula:

Not intuitive as it is, it still may be presented in the form of a geometric diagram:

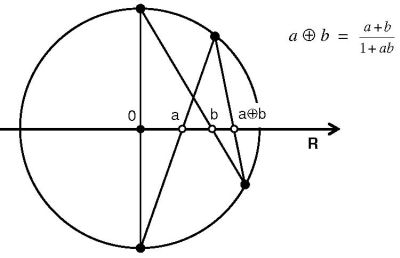
Here is an interactive version of this diagram. Have fun.

More you can read in my preprint. It contains also a diagram for trigonometric tangent, unlike the published version (Am. J. Phys. Aug 2012 80 (8) p. 737.)

Apollonian gasket:   a mathematical microcosm [31 Aug 2012]

Next week it is my turn to tell something at our qolloquium. The above is the title of my talk. Below is the abstract. In a meantime you may want to play with this interactive applet [CLICK on the image to go to a new page]:

Abstract: Quite interestingly, a number of key ingredients of mathematical physics appear in some form in the Apollonian Window, a special case of an Apollonian disk packing. We will present some of its number-theoretic features, analogies with the theory of relativity, and then concentrate on the spinor structure concealed in it. A sequence of theorems will explain the flow of the spinors in the gasket including the topological non-triviality of the spinor fiber bundle over the gasket.

You may also visit my page devoted to the Apollonian Window.
 

∗