Kuratowski's graph K3,3

According to Kuratowski's theorem, a graph is planar (can be represented in a plane without intersections) if and only if it does not contain a subgraph homeomorphic with any of these two:

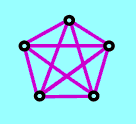
    K₅ --- complete graph of order 5
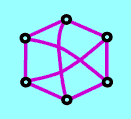
    K_3,3 --- click on the picture for anothe version

The two "forbidden" graphs are called Kuratowski's graphs

The second graph (also called Thompson's graph) K_3,3 is also a theme of a well-known   utility teaser   popularized by Kuratowski's teacher Hugo Steinhouse in his Mathematical Snapshots (Dover; orig. Matematyczny Kalejdoskop, Warsaw).

Kazimierz (=Casimir) Kuratowski (1896--1980, Poland) -- although known mainly as a founder of the modern global topology and the author of the Zorn Lemma -- did also fundamental work in graph theory, reviving the subject. (the "K" of complete graphs actually stands for Kuratowski).

The harmonic evolution digraph for K3,3 consists of:

	Loops	=	16 L1
	Tree	=	T2

The harmonic evolution digraph has the following loop- and tree- parts:

	Loops	=	16 L1
	Tree	=	T1

Home