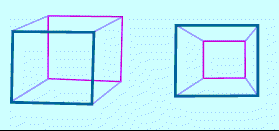
| To draw a 4D cube, let's learn first from drawing a 3D cube: duplicate a 2-cube (square) and then connect corresponding vertices. A special perspective is achieved by locating one square inside the other --- it gives an impression of "looking inside a room through a wall." |

|

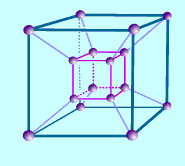
| Similarly, to obtain a 4-cube -- duplicate a 3-cube and connect the corresponding vertices. The result: a 4-dimensional room viewed through a (3D) wall. |
![]()
|
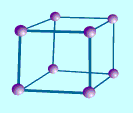
What is the 4D analogue of the "skewed"
perspective of a 3-cube like this? |
|